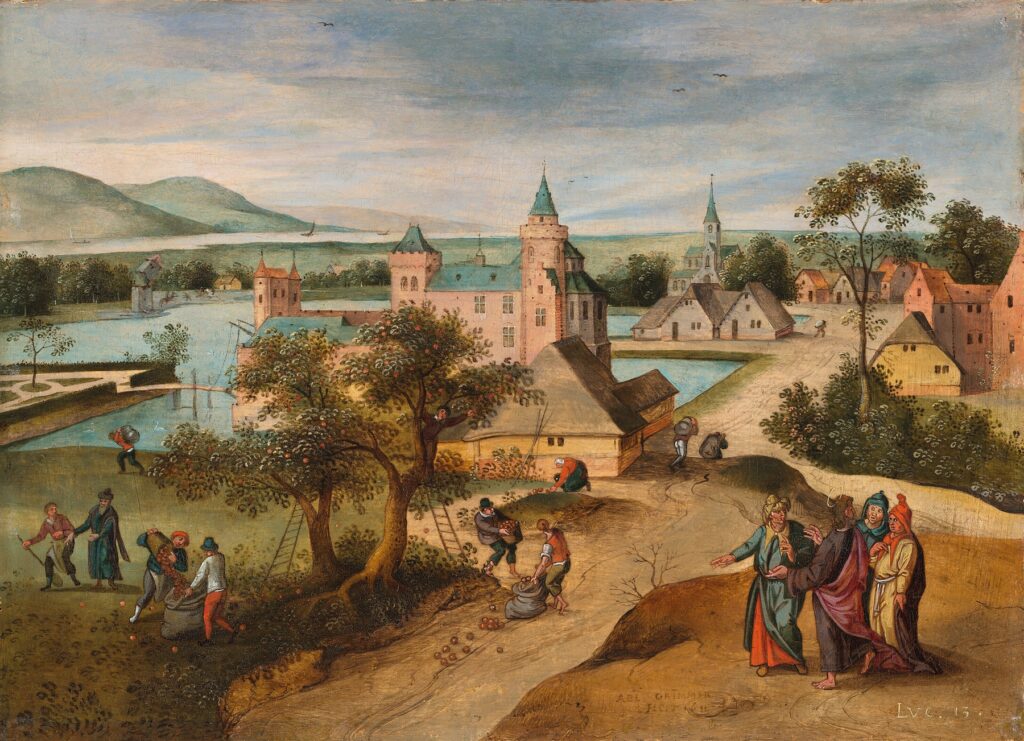
Introduction
For this ThuRsday Tutorial, we’re going to cover something a bit different. Instead of showing how to do fairly simple epidemiological calculations, this edition will cover the first of many Machine Learning and Artificial Intelligence topics: Decision Trees. First, we’re going to cover what Decision Trees are, then do a quick step by step implementation guide in R, and lastly, leave you with a bit of homework should you wish. As usual, if you want to follow along, head over to Cody’s Github to download the article code and data.
What is a Decision Tree?
A decision tree is a type of supervised learning algorithm used for classification and regression tasks. To newcomers that previous sentence may have made very little sense, so let’s break this down. A supervising learning algorithm is a machine learning method that uses data that has at least in part already been reviewed by a human, so the algorithm can learn through reviewing previously tagged data, and test itself against similarly tagged data. Classification is the sorting of data into specific categories (for example, petting pictures of cats and dogs in a “pets” category, while pictures of flowers and trees may be put in a “plants” category), and Regression is a way to estimate future numerical data based on patterns seen in previous numerical data.
A decision tree operates much like the process you might use to make a decision in everyday life—by asking a series of yes/no questions until a conclusion is reached. In the context of machine learning, these questions are based on data and are structured in a tree-like model of decisions.
The Structure of a Decision Tree
- Nodes: Each point in the tree where a question is asked is called a node. The very first question, which starts the decision-making process, is known as the root node. From this point, the tree branches out based on possible answers to the questions posed.
- Branches: Each answer to a question leads to a new branch in the tree. These branches represent the flow from one question to another, guiding the process through more specific inquiries until a final decision can be made.
- Leaves: The leaves of the tree are the end points, representing the outcomes or final decisions. Once a leaf is reached, no further questions are necessary, and the decision tree has provided its prediction or classification based on the inputs given.
Decision trees are built using algorithms that identify the most significant questions to ask at each step. The goal is to select questions that best split the data into distinct categories, making it easier to predict or classify the data as you move deeper into the tree. This process involves statistical methods that measure how well each question separates the data according to the target variable (the outcome we want to predict).
In technical terms, the algorithm selects the questions based on measures like Gini impurity or entropy, which quantify how much uncertainty or “messiness” exists in the categories formed at each step. By choosing questions that reduce this uncertainty the most, the decision tree can efficiently reach accurate decisions.
One practical example of how one could imagine a decision tree is imagining having to sift through hospital visit data to find potential cases of the flu. Say that you know from previous experience what all the symptoms and test results may need to be to be certain of a flu diagnosis (the training section), and you’re given a few records to skim through. You’d likely use a system of yes or no questions, arranged by relative relevance to sort these records.
Does the record indicate a positive flu test? If so, then we can say it’s a flu record, if not, it may not be the flu, and if we don’t have results, we can move down a branch and onto the next node. Does the record indicate fever, aches, or have had recent contact with someone already sick with the flu? Depending on the answer we can use the algorithm to not only have a good idea of which records are flu or not, but also have a standard path to explain our decisions easily.
Now that we have a basic idea of how Decision Trees work, let’s try building one in R.
Building a Decision Tree in R
Project Outline
for this scenario, imagine you’ve been contacted to take a look at some healthcare expenditure data, and to fill in some potentially missing data so that other programs might be able to better estimate the benefits of prevention programs for various conditions prior to surgical intervention in terms of patients seen for said procedures. For this, we’ll be using data from the Health Service Executive , sourced from Open EU Datasets Portal. For this tutorial, the data is also included in the Github repository where the tutorial code is also found. This dataset shows various surgical procedures for the last 20 years or so, how many of these procedures were performed each year, and if there was a break in the reporting series for the year being reported on. By nature of the data, the decision tree will be very simple, and while such a simple use case may not be ideal for this task, the limited variables make it easier to see how these work. In general, you’d want data with more variables that could help explain potential relationships between key factors.
Setting Up in R: Libraries
First, ensure you have the necessary packages installed and loaded. We will use `readr` for data loading, `caret` for data partitioning, and `rpart` for creating the decision tree models.
Data Read-In
We start by loading our dataset and examining its structure. This step helps us understand the types of variables and data formats we are dealing with.
Here, we can see that we’re dealing with character and numerical variables, which is fine to start with. But to be able to make our Decision Tree work out, we’ll need to change a few of these data types around a bit.
Data Preparation
Converting character variables to factors is crucial because many modeling techniques, including decision trees, handle factors differently from other data types. Namely, given that factor data is organized into distinct categories, it can help our Decision Tree organize the questions and answers into a proper tree. Here, we will want to see how the Year , Type of Surgical Procedure and Case Type influence our Value variable, so let’s go ahead and change those to factors.
We also split the data into two subsets based on a flag indicating a break in series, where those with breaks are going to be serving as our implementation dataset, while the rest will be used for training and testing.
Creating Training and Testing Data
For training our model, we create a stratified sample to ensure each category of the surgical procedure is fairly represented in both training and testing sets.
Here we are setting a random seed to pick out what records are retained in training or testing, then breaking the data up based on surgical procedure as mentioned earlier, and creating a 70-30 split for training and testing respectively. We then break those sets up for later use.
Building and Evaluating the Decision Tree Model
We now build our decision tree model using the `rpart` function.
Within `rpart`, we set up an equation of sorts for the Decision Tree to work with where our Value variable is considered to be determined by a mix of our factored variables, where we can train on our predetermined data, and are using ANOVA regression tree models specifically.
Next we can also take a look at how well it’s handled the training data so far, either through various statistical measures using the summary function, or by visually inspecting the resulting tree using both plot for the basic shape, and text to show the variables and associated potential choices and weight.
Even at this point we can see that the Mean Squared Error is very large, and can fairly comfortably be certain this method is less than ideal for this question, but we can still see how it performs against the testing dataset, and go from there.
Improving the Decision Tree
These initial results are not great to say the least, so we might consider several strategies:
– Cross-validation:Helps in understanding how the model performs across different subsets of the data, and can improve results with that understanding.
– Parameter tuning: Adjusting the complexity of the model might help reduce overfitting or underfitting. As a quick note, overfitting refers to when a model can do extremely well on training data, but when introduced to new data which don’t match the exact trends and patterns, tend to fail. Underfitting basically means a generally under-performing model both with training and other data.
With the above script we edit our model call slightly, using a slightly different method and then doing a 10x cross validation. We can then print the results of this validation and get a cp value for the best model. This cp value can then be used to control the specifics of the model and be ran instead of the base model.
We can then go over what we’ve previously done, and finally implement a model on our missing data.Given the data isn’t truly missing, we can look at the Predicted Value and examine it against our actual Value to see how well this model did in both base performance and how the model can explain data relationships.
Conclusion: Next Steps and Future Improvements
Based on the performance and the nature of data, we could consider:
– Including more relevant features that might influence the outcomes.
– Trying different types of models that may fair better for this question (Regression models, XGBoost, etc).
– Revisiting data preprocessing steps to handle outliers, missing values, or transform variables.
– If possible, changing the question to see if end values can be categorical instead of numerical (so under 5000, between 5000-10000, etc), which tends to perform better in tree models.
Feel free to try your hand at improving performance, and use it as a bit of a testing ground. It’s worth noting that with a lot of Machine Learning methods, practicing how and when to implement them is crucial to having a good understanding of methods and their steps.
Humanities Moment
The featured image for this ThuRsday Article is September – The Parable of the Barren Fig Tree (1611) by Abel Grimmer (Flemish, c. 1570–c. 1620). Grimmer was a Flemish late Renaissance painter from Antwerp, known for his landscape paintings and architectural scenes that displayed a trend towards naturalism. Influenced heavily by his father, Jacob Grimmer, and artists like Pieter Bruegel the Elder, Abel developed a style characterized by simplified, schematic compositions with vivid color harmonies, which allowed him to produce work efficiently and affordably for the Antwerp market.
